Pictures in teaching Haskell

Simon Thompson, January 2000

It is useful to give visual portrayals of various programming ideas. The Pictures case study in Haskell: The Craft of Functional Programming, Second Edition attempts to do this. The case study represents ASCII-based pictures as lists of strings (which are themselves lists of characters). The example is used to introduce

This note describes some further material, including

1. Pictures for visualizing recursion over Int

This section presupposes that you have read Sections 4.1 to 4.3 of the text.

How does recursion work over integers? The general pattern is to write a function of the form:

As a skeleton this looks like 
fun :: Int -> ...

fun n
  | n==1    = ...
  | n>0     = ... fun (n-1) ...
and this can come over visually if used with Pictures

A line of black squares

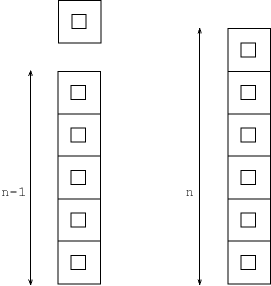
A line of black squares can be built by putting squares side by side. To build a line of n squares, it is enough to put a square sideBySide with (n-1) squares:

so as a recursive definition, 

blackSquares :: Int -> Picture

blackSquares n
  | n==1	= black
  | n>1		= black `sideBySide` blackSquares (n-1)

Lines of black and white squares

Suppose that we want to build a line of alternating black and white squares: a line of length n beginning with a black square is got by sticking a black square on the front of a line beginning with a white square:

and as a definition we have 

blackLine, whiteLine:: Int -> Picture

blackLine n
 | n==1	  = black
 | n>1	  = black `sideBySide` whiteLine (n-1)

whiteLine n
 | n==1	  = white
 | n>1	  = white `sideBySide` blackLine (n-1)

A chess board

Using the lines of the last example it is not hard to build a chessboard. First the diagram:

and as a definition we have 

blackChess:: Int -> Int -> Picture

blackChess n m
 | n==1	 = blackLine m
 | n>1	 = blackLine m `above`
           whiteChess (n-1) m
with an n by n chessboard given by 
chessBoard :: Int -> Picture

chessBoard n = blackChess n n

Exercises

1. How would you define a function to give you a column of pictures, 

picCol :: Int -> Picture -> Picture
as illustrated here

2. Give a Haskell definition of a function which takes an integer n and returns an n by n square which is white apart from a diagonal black line from top left to bottom right:

3. Give a Haskell definition of a function which takes an integer n and returns an n by n square which is white apart from a diagonal black line from top right to bottom left:

4. Give a Haskell definition of a function which takes an integer n and returns an n by n square which is white apart from a black cross joining diagonally-opposite corners:

5. Can you give a direct recursive definition of chessBoard so that 

chessBoard n = ... chessBoard (n-1) ...
Your solution to question 1 might well give you a guide here.

2. Alternative representations of Pictures

This section looks at a variety of different ways that pictures could be represented and the discusses the trade-offs between the various different representations. It forms a useful introduction to the idea that abstract objects like pictures can be represented concretely in a number of different ways. Moreover, it shows that choices can made between the representations in a reasoned way according to what is required by way of picture-manipulating functions.

The current representation: [String].

The picture is represented by a list of lines; each line is a String. The functions we developed over pictures were 
above, sideBySide    :: Picture -> Picture -> Picture
flipH, flipV, rotate :: Picture -> Picture
invertColour         :: Picture -> Picture
superimpose          :: Picture -> Picture -> Picture
printPicture         :: Picture -> IO ()
We'll discuss these functions when looking at the alternatives.

As an example we take the picture 

      ##..#
      ..###
which in the current representation is [ "##..#" , "..###" ].

A single string: String

The example is represented by "##..#\n..###\n", which on the face of it seems the simplest representation.

To place one picture above another, the two strings are joined using ++ (that's why there is a final \n at the end of the string). Similarly to invertColour you just need to invert each character (apart from \n).

However, flipping in a horizontal or vertical mirror is mot easy using this representation, as you need to do things with the individual lines. It is possible, almost, to do rotate by reversing the list. In the example, reversing the list gives 

"\n###..\n#..##"
which is (almost) a representation of 
      ###..
      #..##

A list of columns: [String].

Instead of representing a list of rows, we can represent a picture by the list of columns of the picture. The example becomes: 
[ "#." , "#." , ".#" , ".#" , "##" ]
All the functions over pictures can be implemented over this representation: it is simply that the roles of horizontal and vertical are reversed. For instance, to place two pictures sideBySide the lists of columns are joined using ++; in the original representation above was implemented by ++ and sideBySide thus 
sideBySide pic1 pic2 = [ line1 ++ line2 | (line1,line2) <- zip pic1 pic2 ]

Is there anything to choose between the column representation and the original (row) one? It is only in the function printPicture, which produces a printable version of a picture. It is easier to implement this with rows than with columns, as the natural printing routine prints one row (line) at a time.

A string/int pair: (String,Int).

This is a variant of the second representation, where the string part only contains the characters in the picture, and the integer gives the length of the lines; it is assumed that all the lines in the picture have the same length. The example becomes ("##..#..###" , 5).

The pros and cons are similar to the simple string representation, but this has the slight advantage that splitting the string into lines is slightly simpler when the length of each line is given explicitly.

A more sophisticated representation: run-length encoding: [[(Char,Int)]].

All the representations so far have used a single character to represent each `point' in the picture. It is possible to give a more compact representation of a line, say, by grouping all adjacent equal characters together. The line 
      ###..
is represented by 
[ ('#',3) , ('.',2) ]
and the rotated example picture by 
[ [ ('#',3) , ('.',2) ] ,
  [ ('#',1) , ('.',2) , ('#',2) ] ]
It's interesting to see how the functions over Picture work now. For all the functions 
above, sideBySide
invertColour
flipH, flipV, rotate
exactly the same programs work! This because these programs operate over lists of lines, and this representation simply changes the representation of the individual lines.

The one difficulty is to implement superimpose. Why? Try an example to see the problem.

To convert one of these representations to a string, we can use 

convert :: [ (a,Int) ] -> [a]
convert xs 
  = concat [ replicate n x | (x,n) <- xs ]

A variant: [Int]

An even more compact variant is possible when there are just two colours. We can represent "###.." by [3,2] and ".##.." by [0,1,2,2].

Exercises

1. It is a nice exercise to work out the details of the implementation of the picture-manipulating functions 

above, sideBySide	:: Picture -> Picture -> Picture
flipH, flipV, rotate	:: Picture -> Picture
invertColour		:: Picture -> Picture
superimpose		:: Picture -> Picture -> Picture
printPicture		:: Picture -> IO ()
for each of the representations given in this section.

2. For each of the representations given in this section, define a function 

rotate90 :: Picture -> Picture
which rotates a picture through 90 degrees anticlockwise. Using this, or otherwise, define a function which rotates a picture through 90 degrees clockwise.

3. For each of the representations given in this section, define a function 

frame :: Char -> Picture -> Picture
so that frame ch pic adds a frame of the character ch to the picture pic.

Projects

1. Build further functions to allow

Last modified 24 January 2000.